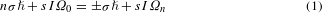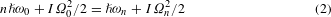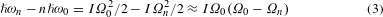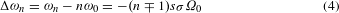Rotational Doppler effect in nonlinear optics
Guixin Li, Thomas Zentgraf & Shuang Zhang
Nature Physics volume 12, pages736–740 (2016)Cite this article
Abstract
The translational Doppler effect of electromagnetic and sound waves has been successfully applied in measurements of the speed and direction of vehicles, astronomical objects and blood flow in human bodies1,2,3,4,5,6,7,8, and for the Global Positioning System. The Doppler effect plays a key role for some important quantum phenomena such as the broadened emission spectra of atoms9 and has benefited cooling and trapping of atoms with laser light10,11,12. Despite numerous successful applications of the translational Doppler effect, it fails to measure the rotation frequency of a spinning object when the probing wave propagates along its rotation axis. This constraint was circumvented by deploying the angular momentum of electromagnetic waves13—the so-called rotational Doppler effect. Here, we report on the demonstration of rotational Doppler shift in nonlinear optics. The Doppler frequency shift is determined for the second harmonic generation of a circularly polarized beam passing through a spinning nonlinear optical crystal with three-fold rotational symmetry. We find that the second harmonic generation signal with circular polarization opposite to that of the fundamental beam experiences a Doppler shift of three times the rotation frequency of the optical crystal. This demonstration is of fundamental significance in nonlinear optics, as it provides us with insight into the interaction of light with moving media in the nonlinear optical regime.
Main
A beam of light with spin angular momentum (SAM) σℏ(σ = ±1), which corresponds to either left or right circular polarization (LCP and RCP) states respectively, flips its spin when it passes through a rotating half-wave plate (HWP). In this process, the circularly polarized light applies a torque on the HWP (refs 14,15) and in return experiences a frequency shift16. For circularly polarized light propagating along the normal axis of a rotating HPW at angular frequency Ω, it was predicted and experimentally confirmed that the transmitted circularly polarized light with the opposite sense has a frequency shift of ±2Ω (Fig. 1a), where the + and − signs correspond to the rotation direction of the HWP, being the opposite or same as that of the circularly polarized incident light16,17,18,19. In recent years, the rotational Doppler effect has been successfully used for probing and controlling the rotation of molecules20, and studying rotating quantum systems21,22. Recently, the observation of the rotational Doppler effect has been extended to light with orbital angular momentum23,24,25,26,27,28, which has shown the capability of remotely measuring the rotational frequency of a spinning object, such as air turbulence, rotating astronomical bodies and so on27.
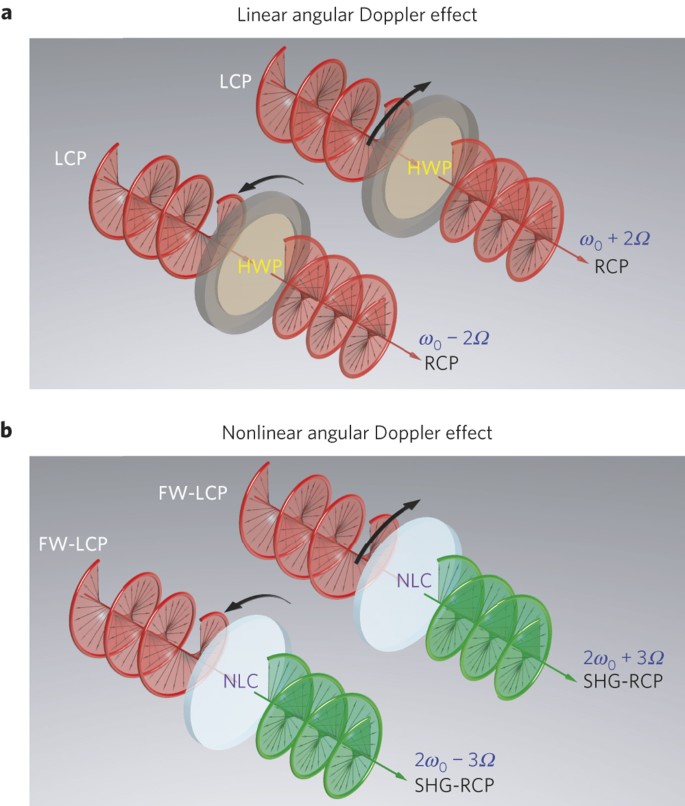
Figure 1: Illustration of the rotational Doppler effect in the linear and nonlinear optical regime.
a, The polarization state of incident light is converted from left circular polarization (LCP) to right circular polarization (RCP) after passing through a half-wave plate (HWP). The linear rotational Doppler shift generates blue- and redshifted frequencies of ±2Ω for the HWP rotating clockwise and anticlockwise (ω0 and Ω are the frequencies of incident light and the angular frequency of the rotating HWP). b, For a left circularly polarized fundamental wave (FW-LCP) passing through the nonlinear optical crystal (NLC) along its three-fold rotation axis, only second harmonic generation (SHG) with RCP state is allowed. The rotation direction of the crystal with the same (anticlockwise) and opposite (clockwise) sense to the handedness of the circularly polarized FW induces frequency shifts of ±3Ω to the SHG light.
Compared with the rapid development and applications of the rotational Doppler effect in linear optics, it has received much less attention in the nonlinear optical regime since it was first predicted for second harmonic generation (SHG) processes more than four decades ago29. So far, the rotational Doppler effect in nonlinear optics has not been observed experimentally. However, the rotational Doppler effect in the nonlinear regime could provide higher sensitivity for the detection of rotational systems due to a stronger dependence on angular frequency. Furthermore, it would impressively demonstrate that the Doppler effect, which is an important fundamental concept in physics, is valid not only in the linear optical regime but also in nonlinear optics.
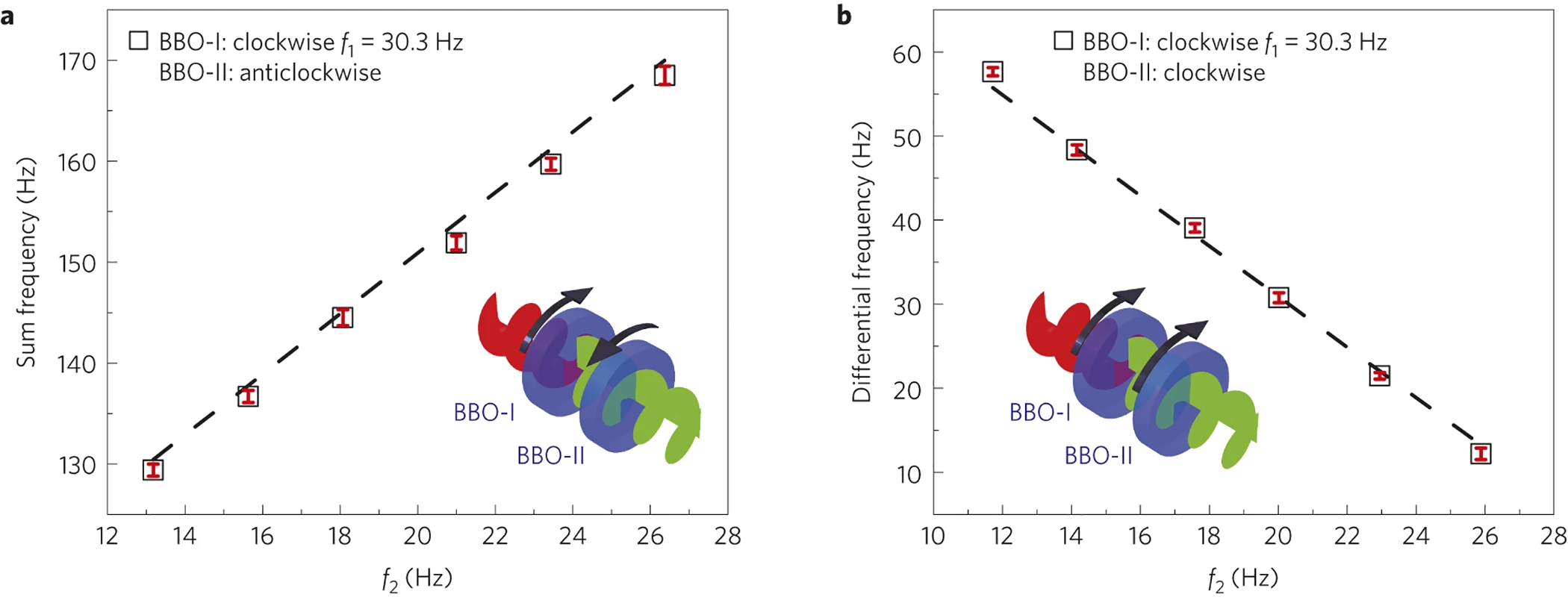
The rotational Doppler effect for harmonic generations can be derived by the consideration of the conservation of energy and angular momentum. In a higher harmonic generation (HHG) process in a rotating nonlinear crystal with a circularly polarized fundamental wave (FW), n photons of fundamental frequency with SAM of σℏ may generate a single photon with SAM of +σℏ or −σℏ at the nth harmonic frequency, where the + and − signs correspond to the harmonic wave with the same and opposite spin as that of the incident FW, respectively. This nonlinear process results in an overall change of −(n − 1)σℏ or −(n + 1)σℏ in the SAM of light for the HHG photon of spin σ or −σ, respectively. At the same time, the change in SAM of photons should be compensated by the change in the angular momentum of the nonlinear crystal. Given that the nonlinear crystal is rotating at an angular frequency of sΩ, where s = ±1 represents the rotation direction and Ω is the amplitude of angular frequency, its angular momentum and kinetic energy are given by L = sIΩ and E = IΩ2/2, respectively, where I is the moment of inertia of the crystal. From the conservation law of angular momentum of the overall system, including both the photons and the rotating crystal, it follows that:
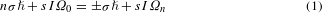
where Ω0 and Ωn are the rotational frequencies of the nonlinear optical crystal before and after the HHG process. We further apply the conservation law of energy, which has to be fulfilled at the same time for the entire system:
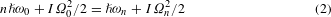
where ω0 and ωn are the frequencies of the FW and the HHG light. From the energy conservation we obtain:
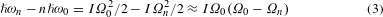
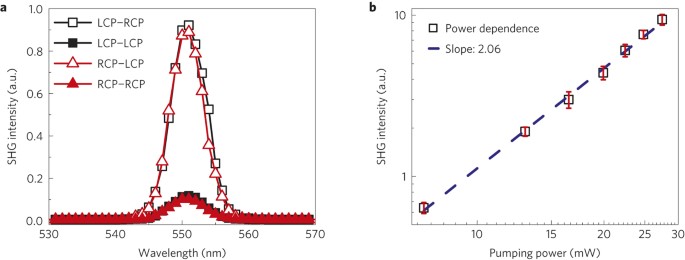
From equation (1) it follows that I(Ω0 − Ωn) = (±1 − n)sσℏ, so by substituting it into equation (3) we finally obtain the nonlinear rotational Doppler frequency shift of the HHG light:
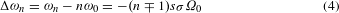
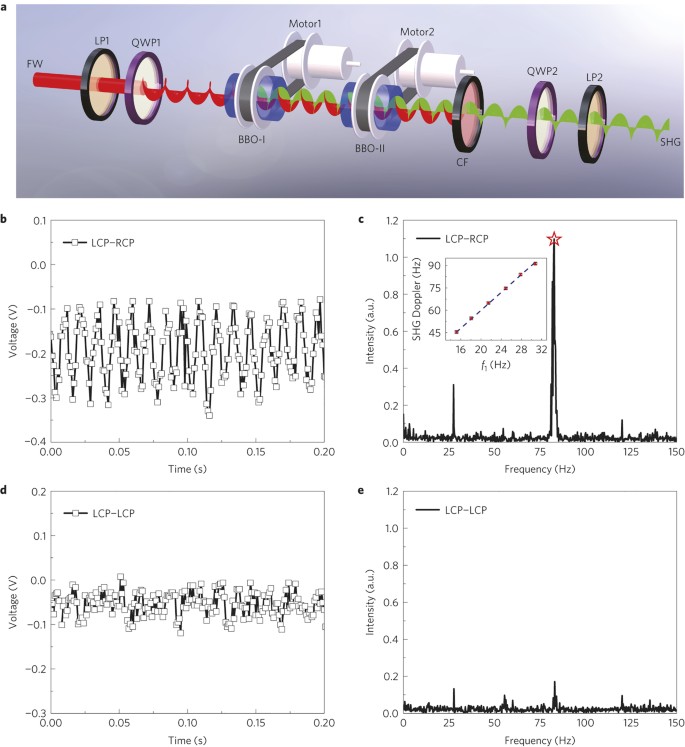
From the derived expression, one can see that the frequency shift of the HHG light is directly proportional to the order of the nonlinear process. Therefore, higher-order nonlinear optical processes will result in larger Doppler shifts. Here, the ∓ sign corresponds to the same or opposite polarization state compared with the FW. Equation (4) also shows that the HHG signal experiences a negative Doppler shift if the rotating direction of the crystal is the same as the spin of incident photons (sσ = + 1), and a positive Doppler shift if the rotating direction of the crystal is opposite to that of the incident photon (sσ = −1).
In this work, we employ a SHG process to verify the theoretical prediction of the rotational Doppler effect in the nonlinear optical regime. For a circularly polarized FW that propagates along the rotation axis of a nonlinear optical crystal with three-fold rotational symmetry, only SHG with opposite circular polarization compared with the FW is allowed29,30,31,32,33,34,35. Hence, for a rotation frequency Ω of the nonlinear optical crystal along its rotation axis (Fig. 1b), the circularly polarized SHG (n = 2) is expected to experience a rotational Doppler frequency shift of:

To test our hypothesis, we carry out measurements of the nonlinear Doppler shift by employing a rotating β-BaB2O4 (β-BBO) crystal, which has a point symmetry of 3m and is being widely used for harmonic generation and optical parametric processes36,37. Note that any other material system with 3m point symmetry could be used in the same way. However, β-BBO has a very high nonlinear susceptibility and provides a suitable platform for our demonstration. By fulfilling the phase-matching condition between the fundamental and the nonlinear wave in type-I and type-II β-BBO crystals, highly efficient SHG with linear polarization can be obtained. However, in both type-I and type-II β-BBO crystals, the strong birefringence effect would result in a continuous variation of the polarization state of the circularly polarized FW along its propagation inside the crystal38,39. This would markedly complicate the measurement of the rotational Doppler effect in the nonlinear regime. In comparison, a circularly polarized FW maintains its circular polarization during its propagation along the three-fold rotation axis of a c-cut β-BBO crystal. Therefore, all experiments are carried out for a propagating wave along the three-fold rotational axis despite the lower conversion efficiency.
First we characterize the SHG from a static β-BBO crystal (Fig. 2a) by using a femtosecond laser (λ = 1,100 nm) with a repetition frequency of 82 MHz and a pulse duration of 200 fs. For a circularly polarized FW propagating along the three-fold axis of a c-cut β-BBO crystal, we find that the SHG signal with the same polarization state as the FW (LCP–LCP and RCP–RCP) is much weaker than that with the polarization state opposite to the FW (LCP–RCP and RCP–LCP). This agrees well with the selection rules for harmonic generations of circularly polarized light demonstrated in previous works29,30,31,32,33,34,35. Theoretically, SHG of the same spin as the FW should be forbidden for a crystal with C3 rotational symmetry. The existence of these weak signals can be attributed to imperfections of β-BBO crystal and slight deviation of the input polarization of the femtosecond laser from circular polarization. For the LCP–RCP measurement, the intensity of the SHG at the wavelength of 550 nm shows a quadratic relationship with the pumping power of FW, which further confirms that the signal is from a second-order nonlinear optical process (Fig. 2b). For a FW (LCP) with an average power of 30 mW, we obtain an efficiency of the SHG (RCP) of around 7.7 × 10−7.
Figure 2: Characterization of second harmonic generation from β-BBO crystal.
a, Measured spectra of the circularly polarized second harmonic generation light. For left- and right- circularly polarized (LCP and RCP) FWs at a wavelength of 1,100 nm passing through the β-BBO crystal along its three-fold rotation axis, the spectra of SHG with both the same (LCP–LCP, RCP–RCP) and opposite polarization states (LCP–RCP, RCP–LCP) compared with that of the FW are measured. The SHG signals for LCP–RCP and RCP–LCP measurements are much stronger (∼eight times) than the SHG signals for the LCP–LCP and the RCP–RCP measurements. This agrees well with the symmetry selection rules for circularly polarized harmonic generations. b, Power dependence of the SHG intensity (open squares) for the LCP–RCP measurement. The result shows a quadratic dependence (dashed line) with slope value: ∼2, which confirms the second-order nonlinear optical process. The error bars represent the minimum and maximum values of SHG intensity for three repeated measurements.
In the second step we measure the rotational Doppler shift of the SHG signal from the rotating β-BBO crystal. Here, we choose a single-pass interferometer design (Fig. 3a) that consists of two cascaded β-BBO crystals rotating by two motors (motor1 and motor2). As the misalignment between the propagation direction of the FW and the c axis of the crystals can introduce optical birefringence and lead to imperfection of the symmetry-selected SHG, we use multi-axis stages to finely tune the angle between the surface normal of the β-BBO crystals and the FW to be less than 0.5° (see Supplementary Methods). The SHG signal passes through a colour filter and is spectrally resolved at a spectrometer before being measured by a photomultiplier tube detector (PMT). The time-dependent SHG signals from the PMT are further amplified by a pre-amplifier and finally sent to a digital oscilloscope for data analysis both in the time and the frequency domains (see Supplementary Methods). Figure 3 shows the resulting interference of the SHG signals that are measured by passing a left circularly polarized FW at the wavelength of 1,100 nm sequentially through the clockwise rotating crystal BBO-I at frequency f1 = 27 ± 0.5 Hz(Ω/2π) and the static crystal BBO-II. The intensity modulations of the SHG signal with the same and opposite polarization states to that of the FW are shown in Fig. 3b, d. We find that the SHG signal in the RCP state exhibits an obvious beating pattern in the time domain, whereas that for the LCP state is more stochastic. By integrating the SHG signals for 50 s and performing a fast Fourier transformation on the digital oscilloscope, we obtain the frequency spectrum for the SHG beating signal (Fig. 3c, e). The dominant frequency peak of the SHG interference is found at fSHG = 82.75 ± 0.8 Hz, which is about three times the rotation frequency of the BBO-I crystal. As shown in the inset plot of Fig. 3c, the beating frequency peak shows a linear relationship with the rotation frequency of the crystal, with a slope of approximately 3, which agrees well with theoretical prediction of rotational Doppler shift for the SHG process given by equation (5). Furthermore, we experimentally verify that the nonlinear rotational Doppler shifts for the SHG are identical for FWs at other wavelengths of 1,150 nm and 1,200 nm (see Supplementary Methods).
Figure 3: Measurement of the rotational Doppler shift for SHG.
a, Schematic illustration of the single-pass interferometer set-up. The left circularly polarized fundamental wave (FW) at wavelength of 1,100 nm is used to illuminate the two cascaded β-BBO crystals (BBO-I and BBO-II), which are mounted in two hollow shafts and can be rotated separately by two motors (motor1 and motor2). The right circularly polarized SHG from BBO-I and BBO-II interferes and is measured by the spectrometer with a PMT detector. The time-dependent signal from the PMT is further amplified and then recorded by a digital oscilloscope. LP1 and LP2, linear polarizers; QWP1 and QWP2, quarter-wave plates; CF, colour filter. b, When the BBO-I crystal is rotating clockwise at frequency f1 = 27 Hz and the BBO-II crystal is static, the SHG interference with opposite spin state to that of FW (LCP–RCP) is measured in the time domain. The SHG signal with the RCP state has a clear intensity modulation. c, Fourier transformation spectrum of the time-dependent signal shown in b. The dominant beating frequency peak (indicated by the red star) corresponds to the nonlinear rotational Doppler shift at a frequency three times the rotational frequency of the BBO-I crystal. Inset: the nonlinear rotational Doppler shift of the SHG signal (squares) for the LCP–RCP measurement shows a linear relationship with the rotating frequency of the BBO-I crystal, with a slope of 3 (dashed line), which agrees well with theoretical prediction. d, The same as in b but for SHG interference with the same spin state as that of FW (LCP–LCP). The LCP-SHG shows only a stochastic fluctuation in time. e, Fourier transformation spectrum of the time-dependent signal shown in d. In contrast with b, there exists no dominant beating frequency peak in the spectrum.
According to equation (4), for the rotating BBO-I crystal, the SHG signals generated by a FW with LCP and RCP states are expected to experience opposite nonlinear rotational Doppler shifts. Likewise, for a FW with a fixed circular polarization state, a β-BBO crystal rotating clockwise and anticlockwise can introduce opposite frequency shifts (Fig. 1). To experimentally observe the existence of opposite nonlinear Doppler shifts for counter-rotating crystals, we rotate the two β-BBO crystals simultaneously in the opposite directions at frequency of f1 and f2, respectively. For this configuration, a sum frequency of the rotational Doppler shifts from the two crystals is expected for the SHG signals. This is confirmed by Fig. 4a, in which the measured beating frequency between the SHG signals from the two crystals satisfies the sum frequency rule: fSF = 3f1 + 3f2. On the other hand, for the two crystals rotating in the same sense, either clockwise or anticlockwise, a difference in frequency shift fDF = 3f1 − 3f2 is observed (Fig. 4b). The observed sum and difference frequency shifts confirm that for given circular polarization of the FW, the sign of the rotational Doppler shift for SHG depends on the rotation direction of the crystal.
Figure 4: Rotational Doppler shift of the SHG as a function of rotation frequency and direction of the β-BBO crystal.
a, Doppler frequency of the SHG signal when the BBO-I crystal is rotating clockwise at frequency f1, and the BBO-II crystal is rotating anticlockwise at frequency f2. b, BBO-I and BBO-II are both rotating clockwise at frequency f1 and f2, respectively. The sum and differential frequencies of SHG rotational Doppler shift for LCP–RCP measurement show a linear relationship with f2, with a slope close to the theoretical value of 3 (dashed line); this indirectly proves the existence of the frequency shifts of the SHG signal for the angular Doppler effect. The definition of rotational direction is identical to the convention used in Fig. 1b. The error bars represent the minimum and maximum values of SHG Doppler shift for three repeated measurements.
It should be noted that in our derivation from equation (1) to equation (4) we have not considered the rotational symmetry of the utilized crystal. Although equation (4) shows that the Doppler shift is directly related to the harmonic generation order, the rotational symmetry of the nonlinear crystal also plays an important role. The reason is that crystals of certain rotational symmetry allow only nonlinear processes of certain orders according to the selection rule pertaining to harmonic generations with circularly polarized FWs33,34. Specifically, it has been shown that the allowed nonlinear generation orders are given by n = ml ± 1, where m is the rotational symmetry order, l is an arbitrary positive integer, and ‘+’ and ‘−’ signs correspond to the harmonic generation signal with the same and the opposite circular polarization as that of the fundamental beam, respectively33. The selection rule, in conjunction with equation (4), leads to the following expression of the rotational Doppler shift in terms of the rotational symmetry of the crystal:

The relationship between the Doppler shift and the rotational symmetry of the crystal is summarized by Supplementary Tables 1 and 2. One can see that although there is a correlation between the rotational symmetry of the crystal and the Doppler frequency shift, there is no one-to-one correspondence between the two. On the basis of equation (6), a three-fold rotationally symmetric crystal (m = 3) introduces a frequency shift 3l (l is an arbitrary integer) times that of the rotating frequency of the crystal. For a FW of spin σ, it can give rise to a 3Ω frequency shift for SHG of spin −σ and fourth harmonic generation of spin σ, a 6Ω frequency shift for fifth harmonic generation of spin −σ and seventh harmonic generation of spin σ, and so on (see Supplementary Tables 1 and 2). Furthermore, a 3Ω Doppler shift can appear for a crystal with either C1 or C3 rotational symmetry for harmonic generations of the second or the fourth order.
To summarize, our experiments for the first time verify experimentally the rotational Doppler shift in the nonlinear optical regime for the SHG. Considering that the SAM of light has recently attracted great attention in nonlinear optics40,41, the nonlinear rotational Doppler shift may find application in characterizing chiral molecules, magnetic materials and probing the strong light–matter interaction in turbulent or spinning media, such as of laser–plasma and molecular systems42.
Methods
SHG measurement.
For the second harmonic generation (SHG) from the c-cut β-BBO crystal (size 5 × 5 × 5 mm3) we used a femtosecond pumped optical parametric oscillator with a repetition frequency of 80 MHz and pulse duration ∼200 fs. The FW with a spot size of 1 mm in diameter is normally incident on the β-BBO crystals. The averaged power of the pumping laser is around 30 mW at a wavelength of 1,100 nm. After filtering the FW by using band-pass filters, the collinear SHG signal along the rotational axis of the BBO crystal was spectrally resolved by an Andor spectrometer (Shamrok 500i) equipped with a photomultiplier (PMT) detector working at room temperature (Supplementary Fig. 1). The measured SHG signals at the PMT detector were further amplified by the pre-amplifier and finally sent to the digital oscilloscope for measurement of the nonlinear rotational Doppler shift. The power of the SHG signal from the β-BBO crystal and FW was measured by using the Newport 2936-R controller with 818-IR and 884-UV diode detectors.
Alignment of the β-BBO crystal and calibration of rotational speed.
For the alignment, we spatially overlap a He–Ne laser beam with the femtosecond laser pulses, passing through the β-BBO crystal along its three-fold rotational axis. If the β-BBO crystal is not perfectly aligned with the femtosecond laser beam, the back-reflection of the He–Ne laser is rotating around the incident light, which is monitored by using a screen (Supplementary Fig. 2). Then the orientation of the β-BBO crystal is finely tuned to minimize the reflection angle of incident light. By such an alignment procedure tilting angles of the β-BBO crystal with less than 0.5° with respect to the laser beam were obtained.
By placing the He–Ne laser beam at the non-centre position of the BBO crystal and mounting a block on the rotating shaft, the intensity of the He–Ne laser has aperiodic modulation. This modulation was then monitored by a Si detector with bandwidth of 2.4 MHz. The voltage signal is recorded by a Keysight 4-channel Oscilloscope with a bandwidth of 200 MHz and sampling rate of 2.5 G samples s−1. The d.c. motor is controlled by using a Keysight programmable d.c. power supply. The maximum rotating frequency of the motor is less than 35 Hz for an 11 volt input. Hence, the bandwidth of the silicon detector and digital oscilloscope are high enough to measure the time-dependent intensity modulations of the He–Ne laser. The rotating frequency of the β-BBO crystal can be instantaneously analysed through the Fourier transformation function of the digital oscilloscope.
Acknowledgements
This work was supported by EPSRC (EP/J018473/1), Leverhulme (grant no. RPG-2012-674), NSFC (grant no. 61328503), the DFG Research Center TRR142 ‘Tailored Nonlinear Photonics: From Fundamental Concepts to Functional Structures.’, and the Opened Fund of the State Key Laboratory on Integrated Optoelectronics No. IOSKL2014KF12. G.L. would like to thank W. Chen and S. Brookes for making the rotators.
Author information
Authors and Affiliations
School of Physics & Astronomy, University of Birmingham, Birmingham B15 2TT, UK
Guixin Li & Shuang Zhang
Department of Physics, University of Paderborn, Warburger Straße 100, D-33098 Paderborn, Germany
Thomas Zentgraf
Contributions
S.Z., G.L. and T.Z. conceived the idea, G.L. performed the experiment, and all authors participated in discussion and writing of the manuscript.
Corresponding author
Correspondence to Shuang Zhang.